Energia mechaniczna, praca, zasada zachowania energii, moc
Wszystkie zasady zachowania są bardzo użyteczne i pomocne z zrozumieniu wielu problemów. Zasada zachowania energii jest potężnym narzędziem ułatwiającym rozwiązać wiele problemów fizycznych. Jej zaletą jest to, że układ fizyczny opisywany jest za pomocą wielkości skalarnych (energie są skalarami), co powoduje, że równania upraszczają się do równań algebraicznych. Prawdopodobnie właśnie to docenił Lagrange, który wymyślił swój własny formalizm (podobnie jak Hamilton). Nie mamy do czynienia z wektorami, dlatego zamiast trudzić się z definicjami kinematycznymi można spokojnie zapisać bilans energetyczny, a ułożone równania dają niemal od razu rozwiązania. Taki przykład pokazałem w temacie Pojęcie siły tarcia.
§ 1. Praca
1.1. Definicja
Praca jest iloczynem skalarnym działającej siły i wektora przesunięcia 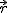 stycznego cały czas to toru ruchu (krzywej po jakiej porusza się ciało).
stycznego cały czas to toru ruchu (krzywej po jakiej porusza się ciało).

Dla dowolnej siły - ogólna definicja
Całka występująca w ostatnim wzorze jest tzw. całką krzywoliniową. Całość symbolizuje pracę wykonaną po dowolnej krzywej od punktu 1 do punktu 2.
Jednostką pracy w układzie SI jest dżul 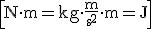 .
Inne powszechnie i dawniej wykorzystywane jednostki pracy i energii:
.
Inne powszechnie i dawniej wykorzystywane jednostki pracy i energii:
- erg (jednostka energii w układzie jednostek Gaussa - CGS)
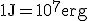
- elektronowolt
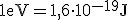
- kilokaloria
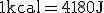
§ 2. Energia kinetyczna
2.1. Definicja energii kinetycznej
Energia kinetyczna jak sama nazwa wskazuje związana jest z poruszającym się ciałem. Energia ta jest zdefiniowana następująco:
Jeśli całość pomnożymy przez 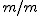 i skorzystamy z definicji pędu:
i skorzystamy z definicji pędu: 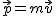 to otrzymamy związek
to otrzymamy związek
2.2. Wyprowadzenie twierdzenia o pracy i energii kinetycznej (tw. P-EK)
Znajdźmy pracę siły wypadkowej działającej na ciało. Załóżmy, że siła ta jest stała. Ciało zatem porusza się ruchem jednostajnie przyspieszonym (lub opóźnionym). Niech 
Skorzystamy z tego, że 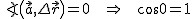 oraz wykorzystamy wzór
oraz wykorzystamy wzór 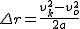 . Wówczas
. Wówczas
Twierdzenie o pracy i energii kinetycznej
§ 3. Pole sił zachowawczych
Na wstępie zaznaczę, że siły zachowawcze (konserwatywne) nie są tym samym co siły potencjalne. Powiedziałbym, że siły zachowawcze są szczególnym przypadkiem sił potencjalnych, co wyniknie z poniższych definicji.
3.1. Definicja siły zachowawczej
Siła zachowawcza to siła, dla której można określić energię potencjalną.
Energia potencjalna z kolei jest szczególnym przypadkiem potencjału 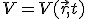 , gdyż jest funkcją, która nie jest w sposób jawny zależna od czasu. Gdyby tak było, byłaby potencjałem. Zatem i siła potencjalna jest szczególnym przypadkiem siły konserwatywnej.
3.2. Warunki jakie musi spełniać siła, by była siłą zachowawczą
Siła działająca na cząstkę jest zachowawcza wtedy i tylko wtedy, gdy spełnia dwa warunki:
, gdyż jest funkcją, która nie jest w sposób jawny zależna od czasu. Gdyby tak było, byłaby potencjałem. Zatem i siła potencjalna jest szczególnym przypadkiem siły konserwatywnej.
3.2. Warunki jakie musi spełniać siła, by była siłą zachowawczą
Siła działająca na cząstkę jest zachowawcza wtedy i tylko wtedy, gdy spełnia dwa warunki:
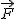 zależy jedynie od położenia cząstki
zależy jedynie od położenia cząstki 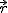 (nie zależy od innych zmiennych - prędkości, czasu i innych)
(nie zależy od innych zmiennych - prędkości, czasu i innych) 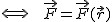 .
. - Praca
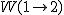 jaką siła
jaką siła 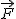 wykonuje wzdłuż krzywej łączącej punkty 1 i 2 nie zależy od wyboru krzywej
wykonuje wzdłuż krzywej łączącej punkty 1 i 2 nie zależy od wyboru krzywej
.
Dlatego na przykład siła Lorentza nie jest potencjalna. Zależy ona od prędkości, zatem dla pola magnetycznego nie można zdefiniować energii potencjalnej.
§ 4. Energia potencjalna
4.1. Definicja energii potencjalnej
Wybierzmy dowolny punkt 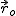 , w którym
, w którym 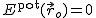 . Energię potencjalną definiujemy jako:
. Energię potencjalną definiujemy jako:
Nam wystarczy wiedzieć jakimi wzorami wyrażają się energie potencjalne dla poszczególnych sił zachowawczych. Na szczęście dla większości podstawowych sił można wskazać energię potencjalną.
Niech energia potencjalna w punkcie 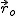 wynosi zero.
wynosi zero.
Z rysunku wynika, że
Związek pracy siły zachowawczej z energia potencjalną
Zapiszmy teraz zasadę zachowania energii mechanicznej:
Zasada zachowania energii dla jednej cząstki Jeśli na ciało działa 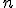 sił
sił 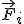 (i=1,2,3,...,n), które są zachowawcze i z każdą z nich związana jest energia potencjalna
(i=1,2,3,...,n), które są zachowawcze i z każdą z nich związana jest energia potencjalna 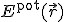 , to całkowita energia mechaniczna, zdefiniowana jako
, to całkowita energia mechaniczna, zdefiniowana jako
nie zależy od czasu.
Przypomnimy teraz wzór na pracę siły wypadkowej. Jest oczywiste, że siła wypadkowa działająca na ciało może składać się zarówno z sił zachowawczych jak i niezachowawczych, zatem:
Wykorzystujemy poznane związki i otrzymujemy:
Jeśli siły niezachowawcze nie wykonują pracy to otrzymujemy bardzo użyteczny związek:
Użyteczny związek dla wszystkich rodzajów sił
§ 5. Sprawność
5.1. Definicja
Sprawność to stosunek energii otrzymanej od układu do energii dostarczonej. Sprawność może być podawana jako zwykła liczba lub za pomocą procentów.
§ 6. Moc
6.1. Definicja mocy
Moc nazywana także szybkością wykonywanej pracy jest stosunkiem pracy do przedziału czasu w jakim ta praca została wykonana.
Moc na ogół zapisuje się wzorem
lub, jeśli zachodzi potrzeba, ściślej
Jednostką mocy w układzie SI jest wat 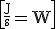 .
Istnieją też inne jednostki mocy
.
Istnieją też inne jednostki mocy
- kilowatogodzina
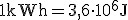
- koń mechaniczny
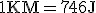
Przykład 1 - Diabelska pętla
Na rysunku dana jest diabelska pętla. Jej główna część jest okręgiem o promieniu 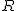 . Z jakiej wysokości należy wypuścić ciało, aby bezpiecznie przejechało przez pętlę? Wszelkie opory ruchu pominąć.
. Z jakiej wysokości należy wypuścić ciało, aby bezpiecznie przejechało przez pętlę? Wszelkie opory ruchu pominąć.
Rozwiązanie:
Zapiszmy zasadę zachowania energii: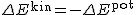 .Rozpatrzmy (jak to zaznaczyłem na rysunku) sytuację początkową - ciało znajduje sie nieruchomo ma wysokości
.Rozpatrzmy (jak to zaznaczyłem na rysunku) sytuację początkową - ciało znajduje sie nieruchomo ma wysokości 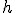 nad powierzchnią Ziemi, którą po cichu uznałem za poziom zerowy energii potencjalnej, i końcową - ciało znajduje sie w najwyższym punkcie okręgu; ma wtedy zarówno energię kinetyczną jak i potencjalną.
nad powierzchnią Ziemi, którą po cichu uznałem za poziom zerowy energii potencjalnej, i końcową - ciało znajduje sie w najwyższym punkcie okręgu; ma wtedy zarówno energię kinetyczną jak i potencjalną.
Zatem zasada zachowania energii ma postać:
Teraz należy się zastanowić jaki warunek ma spełniać szybkość, aby ciało spokojnie przeleciało przez pętlę. Zróbmy to w układzie nieinercjalnym. Aby ciało nie spadało siła odśrodkowa musi równoważyć siłę ciężkości: 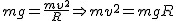 i wstawiając to do równania zasady zachowania energii:
i wstawiając to do równania zasady zachowania energii: 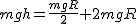 otrzymujemy
otrzymujemy 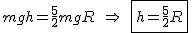 .
.
Przykład 2
Ciała porusza się po półkuli jak pokazuje rysunek. Jego początkowe położenie to 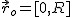 . Na jakiej wysokości ciało oderwie się od półkuli? Pominąć wszelkie opory ruchu.
. Na jakiej wysokości ciało oderwie się od półkuli? Pominąć wszelkie opory ruchu.
Rozwiązanie:
Najpierw należy zbadać warunek przy jakim ciało oderwie się od półkuli. Warunek jest prosty: siła reakcji od półkuli musi być równa zeru. Wtedy i siła nacisku na półkulę będzie równa zeru, zatem ciało oderwie się od półkuli.
Składowa prostopadła do powierzchni półkuli 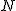 pomniejszona o siłę reakcji
pomniejszona o siłę reakcji 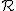 stanowi siłę dośrodkową dla zsuwającego się ciała (oczywiście do momentu oderwania się ciała).
stanowi siłę dośrodkową dla zsuwającego się ciała (oczywiście do momentu oderwania się ciała).
Z rysunku łatwo zauważyć wypatrzyć, że 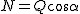 . Skoro
. Skoro 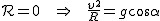 .
Zapiszmy teraz zasadę zachowania energii. Od razu przejdę do równania, nie bawiąc się w oczywiste wyznaczanie zmian poszczególnych rodzajów energii - jak robiłem to w poprzednim przykładzie.
.
Zapiszmy teraz zasadę zachowania energii. Od razu przejdę do równania, nie bawiąc się w oczywiste wyznaczanie zmian poszczególnych rodzajów energii - jak robiłem to w poprzednim przykładzie.
Trzeba wyznaczyć prędkość, ale najpierw warto zapisać 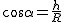 oraz
oraz 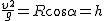 , czyli
, czyli 